eğitim öğretim ile ilgili belgeler > konu anlatımlı dersler > matematik dersi ile ilgili konu anlatımlar

KÖKLÜ SAYILAR, KÖKLÜ İFADELER, KÖKLÜ SAYILARIN ÖZELLİKLERİ (1) İLE İLGİLİ KONU ANLATIMLAR (MATEMATİK DERSİ İLE İLGİLİ KONU ANLATIMLAR, ÖRNEKLER, ÇÖZÜMLÜ SORULAR)

n, 1 den büyük bir sayma sayısı olmak üzere,

xⁿ = a denklemini sağlayan x sayısına a nın n inci dereceden kökü denir.

 

Üslü ifadelerde negatif veya pozitif reel sayıların tam sayı olan kuvvetlerini tanımlamıştık. Bir üslü ifadenin değerini bulmayı biliyoruz.

 

Örneğin:

(-2)²=(-2).(-2)=4,           (2)=2.2=4 tür.

 

A bir reel sayı ve m, 1’den büyük bir tamsayı ^mÖa sayısına a sayısının m inci kuvvetten kökü denir.

 

Burada karesi 4 olan iki reel sayı vardır. Bunlardan negatif olanı (-2), pozitif olanı da (+2) dir. Bunun gibi karesi 9 olan sayılar (-3) ve (+3) tür. Fakat karesi -4 ve -3 olan reel sayı yoktur. Genelleyecek olursak; "xÎR⁺ için karesi x olan biri negatif diğeri pozitif iki reel sayı vardır. Değeri ve üssü verilen üslü ifadelerin tabanını bulma işlemine kök alma işlemi denir.

 

TANIM:karesi aÎR+ e eşit olan iki sayıdan negatif olanına a nın negatif karekökü, pozitif olanına a nın pozitif karekökü denir. Negatif karekök “-Öa”; pozitif karekök “Öa” ile gösterilir. Yani(Öa)²=(-Öa)²=a dır.

Örneğin; x²=16 nın pozitif karekökü x=Ö16=4, negatif karekökü x=-Ö16=-4

(Öa)²=Öa² ifadesi bazen “a” ya eşit değildir. Örneğin;

Öa² ifadesi daima pozitiftir. Öa²³0 olur.

Ö4=2 nin doğru olduğuna, Ö4=-2 nin yanlış olduğuna dikkat ediniz.

B. KÖKLÜ İFADELERİN ÖZELİKLERİ

1) n tek ise, daima reeldir.

2) n çift ve a < 0 ise, reel sayı belirtmez.

3) a  0 ise, daima reeldir.

4) a  0 ise,

5) n tek ise,

6) n çift ise,

7)

8) n çift ve b ile c aynı işaretli olmak üzere,

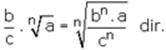
9) n tek ise,

 

10) a, pozitif reel (gerçel) sayı olmak üzere,

 

11) k pozitif tam sayı ve a pozitif gerçel sayı olmak üzere,

12) (a  0 ve b  0)  ise,

 

Teorem:bir reel sayının karesinin karekökü o reel sayının mutlak değerine eşittir.

"xÎR için Öx²=½x½ tir.

 

İspat;

1.      x³0 için ½x½ve Öx² =x tir. o halde, Öx² =½x½olur.

2.      x<0 için ½x½=-x ve Öx² =-x tir. (-x>0) o halde, Öx² =½x½olur.

 

Örnek: x<2 ise  Öx² -4x+4 ifadesi neye eşittir?

Çözüm: Öx² -4x+4 = Ö(x-2)² = ½x-2½(Öx² =½x½)

X<2 ise x-2<0 olur. Bu durumda, ½x-2½=-(x-2)=-x+2 bulunur.

 

Örnek: x<0<y ise Öx²+Öy²-Ö(x-y)² işleminin sonucunu bulunuz.

Çözüm: Öx² = ½x½, Öy² =½y½ ve Ö(x-y)² =½x-y½ dir.

X<0 Þ½x½=-x

Y<0 Þ½y½=y

X<y Þ x-y<0 Þ ½x-y½=-(x-y)=-x+y dir.

Öyleyse, Öx²+Öy²-Ö(x-y)² =½x½+½y½-½x-y½=-x+y+x-y=0 bulunur.

 

Örnek: 3<x<4 ise Öx²-8x+16 +Öx²-6x+9 -½3-x½işleminin sonucunu bulunuz.

Çözüm: Öx²-8x+16 =Ö(x-4)² =½x-4½, Öx²-6x+9 =Ö(x-3)² =½x-3½ tür.

X<4 Þ x-4<0 olup ½x-4½=-x+4 ve

x>3 Þ x-3>0 olup ½x-3½=x-3 olur.

x>3 Þ ½3-x½=-3+x tir.

Öx²-8x+16 +Öx²-6x+9 -½3-x½=½x-4½+½x-3½-½3-x½=-x+4+x-3-(-3+x)

=1+3-x=4-x bulunur.

 

 

KAREKÖKLÜ İFADELERDE TOPLAMA VE ÇIKARMA İŞLEMLERİ

 

Kareköklü ifadeleri toplamak veya çıkarmak için kök içindeki terimler benzer olmalıdır. Benzer olan terimlerin kat sayıların toplamı veya farkı, o terimlere kat sayı olarak yazılır.

Kök dereceleri birbirine eşit ve kök içindeki sayılar da birbirine eşit olan ifadelerin kat sayıları toplanır ya da çıkarılır.

Bulunan sonuç köklü ifadenin kat sayısı olur.

Örnek:

 

aÖb -cÖb +dÖb =Öb(a-c+d) olur.

 

Örnekler:

 

1.      3Ö3-4Ö3+7Ö3=(3-4+7).Ö3

2.      Ö75 -2Ö48 -3Ö27 =2Ö25.3 -2Ö16.3 -3Ö9.3 =2.5Ö3 -2.4Ö3 -3.3Ö3

=10Ö3 -8Ö3 -9Ö3 =(10-8-9)Ö3 =-7Ö3

3.      Ö5/3+2Ö5-3Ö5/2 =(1/3+2-3/2)Ö5 =(2+12-9/6)Ö5 =5/6Ö5

 

Örnek:

işleminin sonucu kaçtır?

 

 

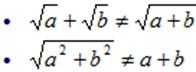
EŞLENİK İFADELERİN ÇARPIMI

1) Kök dereceleri eşit ise kök içleri çarpılır.

 

Örnekler

 

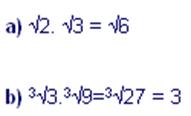
2) Kök içleri eşit ise önce uslu sayıya çevrilir.

 

n ve m, 1 den büyük tek sayı ya da a ve b negatif olmamak üzere, bilgiyelpazesi.com

 

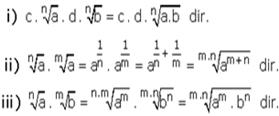
a,bÎR⁺ için

1. Öa nın eşleniği Öa dır.

2. Öa +Öb nin eşleniği Öa-Öb dir.

 

Çarpımları rasyonel olan iki irrasyonel ifadeden her birine diğerinin eşleniği denir. Eşlenik iki ifadenin çarpımı, birinci terimin karesinden ikinci terimin karesinin farkına eşittir. Çarpma işleminin toplama işlemi üzerine dağılma özelliği kullanılırsa,

 

(Öa+Öb)(Öa-Öb)=Öa(Öa-Öb)+Öb(Öa-Öb)=a-Öab +Öab –b=a-b olur.

 

Örnek:

 

1.      (Ö5 -2Ö3)(Ö5 +2Ö3)= Ö5(Ö5 +2Ö3)-2Ö3(Ö5 +2Ö3)=5+2Ö15 -2Ö15 -4.3=-7

2.      (4+2Ö7)(4-2Ö7)=4²-(2Ö7)²=16-28=-12

3.      (x+Ö5)(x-Ö5)=(x²)-( Ö5)²=x²-5 olur.

 

PAYDAYI RASYONEL YAPMA

 

Paydası rasyonel olmayan bir köklü ifadenin paydasını rasyonel yapmak için paydanın eşleniği ile pay ve paydayı çarparız.

 

Örnek:

1.      3/Ö3=3. Ö3/Ö3. Ö3=3Ö3/Ö32=Ö3

2.      1/Ö5-Ö3=1.( Ö5+Ö3)/ (Ö5-Ö3)( Ö5+Ö3)= Ö5+Ö3/(Ö5)²-(Ö3)²=Ö5+Ö3/5-3=Ö5+Ö3/2

3.      7/2Ö2-1=7(2Ö2+1)/(2Ö2-1)(2Ö2+1)=7(2Ö2+1/(2Ö2)²-(1)²=7(2Ö2+1)/8-1=7(2Ö2+1)/7

=2Ö2+1

 

 

 

KAREKÖKLÜ BİR İFADENİN SADELEŞTİRİLMESİ

 

Örnek: (Öa³)⁶.( Öa^-3)⁴ ifadesini sadeleştiriniz.

Çözüm: a^-3=1/a³ yazılabileceğini biliyoruz.(x-n=1/xn kuralına göre)

(Öa³)⁶.( Ö1/Öa³)⁴=Öa¹⁸. Ö1/Öa¹²=Öa¹⁸.1/a¹²=Öa⁶=Ö(a³)² =½a³½ bulunur.

 

Örnek: Öab-3c-2 . Öab5c3 ifadesini sadeleştiriniz.

Çözüm: Öab-3c-2 . Öab5c3 =Öa2b5c3/Öb3c2 =Öa2b2c =½ab½.Öc bulunur.

 

KAREKÖKLÜ İKİ TERİMİN ÇARPIMI

 

a ³0 ve b>0 olmak üzere a,b Î R için Öa.Öb=Öa.b dir.

Kareköklü iki terimin çarpımı, bu terimlerin çarpımının kareköküne eşittir.

 

Örnek:

1.      Ö3. Ö5 =Ö3.5 =Ö15

2.      2Ö3. 3Ö2 =(2.3). Ö3.2 =6Ö6

3.      Ö3. Ö6. Ö2 =Ö3.6.2 =Ö36 =6

 

KAREKÖKLÜ İKİ TERİMİN BÖLÜMÜ

 

a ³0 ve b>0 olmak üzere a,b Î R için Öa/Öb =ÖA/B dir.

Kareköklü iki terimin bölümü, bu terimlerin bölümünün kareköküne eşittir.

 

Örnek:

1.      Ö60 /Ö15 =Ö60/15 =Ö4 =2

2.      Öx⁷/Öx⁵=Öx⁷/x⁵ =Öx² =½x½

3.      Ö21/Ö7 =Ö21/7=Ö3

 

KAREKÖKLÜ BİR TERİMİN n. KUVVETİ

 

Kareköklü bir terimin “n.” Kuvveti bulunurken, verilen ifadenin karekökü alınarak terimin “n.” Kuvveti bulunur ve ele edilen terimin karekökü alınır.

xÎR+ ve n ÎZ+ olmak üzere, (Öx)ⁿ=Öxⁿ ir.

 

İspat: xÎR⁺, nÎZ⁺ için Öx in “n.” Kuvveti,

(Öx)ⁿ=Öx. Öx. Öx…Öx=Öx.x.x…x =Öxⁿ olur.

 

Örnek:

1.      (Ö5)⁴=Ö5⁴=Ö(5²)²=5²=25

2.      (Ö3)³.( Ö6)⁵=Ö3³ . Ö6⁵ =Ö3³(2.3)⁵ . Ö3³.2⁵.3⁵ =Ö3⁸.2⁵

=Ö(3⁴)².(2²)².2=3⁴.2². Ö2 =324Ö2

3.      (Ö1/2)^-4=Ö1/2^-4 =Ö2⁴ =Ö(2²)² =2² =4

 

REEL SAYILARIN RASYONEL KUVVETİ

 

Tanım: a³0 reel sayısı verilsin. n ÎZ⁺ için xn=a olacak şekilde bir xÎR+ sayısı varır.

Bu sayıyı a nın “n.” Kuvvetten kökü denir ve xn =a Û x=ⁿÖa biçimine gösterilir.

 

x2=m eşitliğini gerçekleyen x=Öm değerine, karekök m,

x3=m eşitliğini gerçekleyen x=³Öm değerine, küpkök m,

x4=m eşitliğini gerçekleyen x=⁴Öm değerine, 4. dereceden kök m denir.

 

Şimdide ⁿÖa^m biçimindeki bir ifadeyi üslü şekle yazalım. m=k.n alalım:

 

ⁿÖa^m =ⁿÖa^n.k =ⁿÖ(a^k)ⁿ =a^k dır.

 

m=k.n Þk=m/n dir. ak da k yerine m/n yazalım. a^k =a^m/n bulunur. O halde, ⁿÖa^m=a^m/n dir.

 

örnek:

1.      Öx =x^1/2

2.      ³Öx² =x^2/3

3.      ⁴Ö(x+y)³ =(x+y)^3/4

 

köklü bir terimi üslü biçimde yazarken, terimin üssü pay, kökün derecesi payda alınarak elde edilen rasyonel sayı verilen terime üs olarak yazılır.

 

xⁿ=a denkleminde n tek doğal sayı ise çözüm kümesi: x=ⁿÖa dir.

xⁿ=a denkleminde n çift doğal sayı ise çözüm kümesi: x=±ⁿÖa dır.

 

öyleyse, x=ⁿÖa ifaesi,

 

1.      n tek doğal sayı ve x reel sayıdır.

2.      n çift doğal sayı ve a³0 ise x reel sayıdır.

3.      n çift doğal sayı ve a<0 ise x reel sayı değildir.

 

⁷Ö-128, ³Ö-27, ⁵Ö-1 sayıları reel sayıdır.

Ö25, ⁴Ö16, ⁴Ö8 sayıları reel sayılardır.

Ö-1, Ö-4, Ö-9 sayıları reel sayı değildir.

 

KÖKLÜ BİR TERİMİN KUVVETİ

 

nÖa gibi köklü bir terimin “m.” Kuvveti, (ⁿÖa)^m = ⁿÖa.ⁿÖa.ⁿÖa…ⁿÖa = ⁿÖa.a.a…a=ⁿÖa^m olur.

Öyleyse, (ⁿÖa)^m = ⁿÖa^m dir.

 

Örnek:

1.      (³Öx.y)² =³Ö(x.y)² =³Öx².y²

2.      (³Öa)⁴=³Öa⁴ =³Öa³.a=a³Öa (ⁿÖaⁿ.b=aⁿÖb dir. )

3.      (⁵Ö4)³ =⁵Ö4³=⁵Ö(2²)³ =⁵Ö2⁶=⁵Ö2⁵.2 =2⁵Ö2

 

KÖKLÜ BİR TERİMİN KÖKÜ

 

Bir terimin “m.” Kuvvetten kökünün tekrar “n.” Kuvvetten kökü, bu terimin (m.n) inci kuvvetten köküne eşittir. nÖx in tekrar “m.” Kuvvetten kökü: ^mÖⁿÖx =^m.nÖx dir. Bu eşitliğin doğruluğunu gösterelim:

 

^mÖⁿÖx=(ⁿÖx)^1/m =ⁿÖx^1/m =(x^1/m)^1/n =x^1/m.n =^m.nÖx olur.

 

Öyleyse, ^mÖⁿÖx =^m.nÖx tir.

 

Örnekler:

1.      ³Ö⁴ÖÖa³ =³Ö^4.2Öa³ =³Ö⁸Öa³ =²⁴Öa³ =⁸Öa

2.      ⁴Ö5Ö5³Ö5² =^4.2.3Ö(5²)³.5³.5² =²⁴Ö5⁶.5³.5² =²⁴Ö5¹¹ bulunur.

 

KÖKLÜ İFADELERİN ÇARPILMASI

 

Kök kuvvetleri aynı olan ifadelerin çarpımı, bu ifadelerin çarpımının aynı kuvvetten köküne eşittir.

 

Teorem: a,b ÎR⁺ ve n ÎN⁺ ise ⁿÖa.ⁿÖb =ⁿÖa.b dir.

İspat: ⁿÖa.ⁿÖb =ⁿÖa.b dir. eşleniğinin her iki yanının n. Kuvvetini alalım.

(ⁿÖa.ⁿÖb)ⁿ =(ⁿÖa.b)ⁿ Þ(ⁿÖa)ⁿ.(ⁿÖb)ⁿ =a.b ve (ⁿÖa.b)ⁿ =ⁿÖaⁿ.bⁿ =a.b dir.

 

Örnek: ³Ö2a. ³Ö4a² işleminin sonucunu bulunuz.

Çözüm: ³Ö2a.³Ö4a² =³Ö2a.4a² =³Ö8a³ =³Ö2³a³ =³Ö(2a)³=2a dır.

 

Teorem: x,y ÎR⁺, m,n,k ÎZ⁺ olmak üzere  1. ⁿÖx^m =^n.kÖx^m.k    2. ⁿÖx^m=^n/kÖx^m/k

3.^mÖx.ⁿÖy=^m.nÖxⁿ.^m.nÖy^m=^m.nÖxⁿ.y^m   4. ^mÖx/ⁿÖy=^m.nÖxⁿ/^m.nÖy^m=^m.nÖxⁿ/y^m dir.

 

kök kuvvetleri farklı olan köklü ifadeleri çarpmak için önce kök kuvvetleri eşitlenir sonra çarpma işlemi yapılır.

 

KÖKLÜ İFADELERİN BÖLÜNMESİ

 

Kök kuvvetleri aynı olan köklü iki ifadenin bölümü, bu ifadenin bölümlerinin aynı kuvvetten köküne eşittir.

 

Teorem: a,b ÎR⁺ ve nÎN⁺ ise ⁿÖa/ⁿÖb =ⁿÖa/b ir.

İspat: her iki tarafın  n. Kuvvetten kökünü alalım:

(ⁿÖa/ⁿÖb)ⁿ =(ⁿÖa/b)ⁿ Þ (ⁿÖa)ⁿ/(ⁿÖa)ⁿ  =a/b Þa/b=a/b dir.

 

Örnek:

1.      Ö18a⁵/Ö2a³ =Ö18a⁵/2a³ =Ö9a² =3a dır.

2.      ³Ö54a⁴b⁵/³Ö2ab² =³Ö54a⁴b⁵/2ab² =³Ö27a³b³ =3ab dir.

 

 

Karekök İçindeki İfadenin Kök Dışına Çıkarılması:

 

Karekök içinde çarpım veya bölüm durumunda verilen ifadeler, 2 veya 2’nin katı kuvvetinde yazılabilirse karekök dışında çıkarılabilirler.

Öa^2m = a^m

Öa² . b²  = a . b

 

Örnek: Ö4 = Ö2 = 2^2/2 = 2

 

 

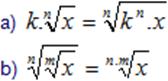
Örnek:

Aşağıdaki irrasyonel sayılardan hangisinin yaklaşık değeri bilinirse  sayısının yaklaşık değeri bulunabilir?

 

 

 

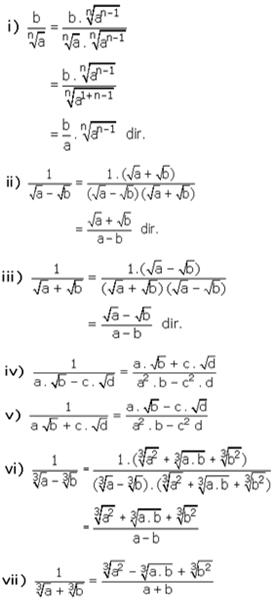
Ondalık Sayıların Karekökü:

 

Ondalık sayıların virgülden sonraki basamak sayıları çift ise tam karekökleri olabilir.

 

Örnek:  Ö0,04 sayısının eşitini bulalım.

 

Çözüm: Ö0,04 ₌ Ö4  ₌ 2 ₌ 0,2

100  10

 

Karekök dışındaki çarpanın kök içine alınması:

 

Kareköklü sayının katsayısının kök içine almak için katsayısının karesini kök içindeki sayı ile çarpar, kök içine yazarız.

aÖb = Öa² .b

 

Örnek: 2Ö3 = Ö2² . 3 = Ö4 . 3 = Ö12

 

Kareköklü sayının n. kuvveti kök içindeki sayının n. kuvvetidir.

(Öa)ⁿ = Öaⁿ

 

Örnek: (Ö7)² = Ö7² = 7

 

Sonsuz Kökler, Sonsuza Giden Köklü İfadeler:

 

 

 

 

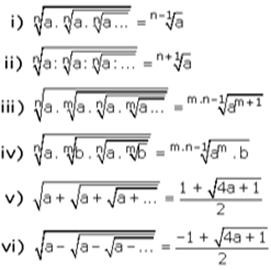
Yukarıdaki son iki özelikte a, ardışık iki pozitif tam sayının çarpımı ise, v. nin cevabı bu sayıların büyüğü, vı. nın cevabı bu sayıların küçüğüdür.

 

 

KÖKLÜ İFADELERDE SIRALAMA

Kök dereceleri eşit olan (ya da eşitlenen) pozitif sayılarda, kök içindeki sayıların büyüklüğüne göre sıralama yapılır.

 

KÖKLÜ İFADENİN EŞLENİĞİ

 

 

 

“MATEMATİK DERSİ İLE İLGİLİ KONU ANLATIMLAR” SAYFASINA GERİ DÖNMEK İÇİN

>>>TIKLAYIN<<<

“MATEMATİK DERSİ İLE İLGİLİ TEST SORULARI, SORU BANKASI” SAYFASINI GÖRMEK İSTERSENİZ

>>>TIKLAYIN<<<

“MATEMATİK DERSİ İLE İLGİLİ YAZILI SORULARI” SAYFASINI GÖRMEK İSTERSENİZ

>>>TIKLAYIN<<<