Eğitim Öğretim İle İlgili Belgeler > Konu Anlatımlı Dersler > Matematik Dersi İle İlgili Konu Anlatımlar

ORAN, ORANTI, ORTALAMALAR, ÇEŞİTLERİ, ÖZELLİKLERİ İLE İLGİLİ KONU ANLATIM (MATEMATİK DERSİ İLE İLGİLİ KONU ANLATIMLAR, ÇÖZÜMLÜ ÖRNEKLER, SORULAR)

En az birisi sıfırdan farklı olmak üzere, aynı birimden iki çoklugun karsılastırılmasına (bölünmesine) oran denir.

Çoklukların aynı birimden olması önemlidir. Litre ile kilometrenin, kilogram ile metrenin birbirlerine bölümü mümkün degildir. Yani, 2 kilogramın 500 grama oranı

degildir.

Birimlerini aynı hale getirdikten sonra bunları birbirine bölmeliyiz.

2 kilogram = 2000 gram oldugundan oranın dogru degeri 2000/500 = 4 olmalıydı.

İste bunun gibi

ifadeleri birer orandır.

Ama

ifadesi bir oran degildir.

Orana yaptıgımız tanıma tekrar bakarsanız kıyaslanan çoklukların en az birinin sıfırdan farklı olması gerektigini söylemis oldugumu göreceksiniz.

İki veya daha çok oranın esitligine orantı denir.

birer oran olmak üzere,

esitlikleri birer orantıdır. İlk orantıya ikili orantı, ikincisine ise üçlü orantı denir.

Burada k degerine orantı katsayısı veya orantı sabiti denir.

orantısında

’tür.

orantısı

a : b = c : d = e : f

şeklinde de yazılabilir.

Nerdeyse ilkokuldan beri bir orantıda içler ile dıslar çarpımının sabit ve birbirlerine esit oldugunu biliriz. Ama niyeyse çogumuz içler hangileri, dıslar hangileri bunu bilmeyiz.

Halbuki bir soru sorulsa ve ‘içlere 2’ser ekleyip, dıslardan 3’er çıkardıgımızda…’ diye baslasa ne yapacagız?

Sorulmadı diye sorulmayacak degil ya! Ayrıca sorulmayacagını bilsek bile ne farkeder ki? Hiç mi insan merak etmez? Demek bugüne kadar etmemisiz.

Ögrenelim:

orantısını a : b = c : d seklinde yazmak mümkündü. İste bu orantıda iç tarafta kalan b ile c degerlerine orantının içleri, dıs tarafta kalan a ve d degerlerine de orantının dısları denir.

İçler ile dısları ögrendik, peki bunların kendi aralarında çarpımları hep esitti, o niye, simdi onu ögrenelim.

oldugundan a = b.k ve c = d.k olur.

İçler çarpımı b.c yani b.(d.k), dıslar çarpımı da a.d yani (b.k).d oldugundan a.d = b.c = b.d.k esitligi de kanıtlanmıs olur.

Bir orantıda digerleri yerinde dururken içler kendi arasında yer degistirebilir. Aynısını dıslar da yapabilir.

Dolayısıyla hem içler hem de dıslar kendi aralarında yer degistirebilirler. Orantı bozulmaz, hala dogrudur fakat orantı sabiti degisebilir.

Bu, orantının yanlıs oldugu anlamına gelmez.

Yani;

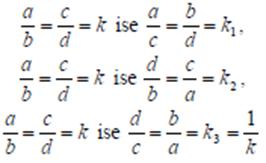
orantısında

a, b, c, d sayılarına sırasıyla orantının birinci, ikinci, üçüncü, dördüncü terimi (elemanı) denir.

Bundan dolayı a, b, c sayılarıyla dördüncü orantılı olan sayı soruldugunda a : b = c : x denklemini saglayan x degerini cevap olarak vermeliyiz.

Bunun yanında a : x = x : b orantısında x degerine de a ile b’nin orta orantısı denir.

oldugunu çoktan anlamıssınızdır

Zaten bu degere a ile b’nin geometrik ortası dendigini de ilerde ögrenecegiz.

Simdi orantılarda ne gibi oynamalar ne gibi sonuçlar dogurur, buna iliskin bazı seyler ögrenelim.

Hangi tür oynamalara izin var, hangilerine yok?

Bu oynamaların hangisi veya hangileri orantı sabitini değiştirmez, hangileri değiştirir?

Değiştirirse ne kadar değiştirir, bunu bilebilir miyiz?

Mesela, durup dururken orantıdaki tüm terimlerin karelerini alalım. Bir sey olur mu?

Olursa ne olur?

Genel olarak kare almayıp da, her terimin n’inci kuvvetini alsaydık orantı sabiti kn olurdu. Aklın yolu bir!

Peki, yine can sıkıntısından payların hepsini toplasak, sonra da paydaların hepsinin toplamına bölsek, bir sey olur mu?

Bakalım:

olur ki bu oynamanın orantı sabitini değiştirmediğini anlarız. Bu çok çok önemli bir kuraldır.

Sadece bu kuralın bilinmesi onlarca sorunun çözümünü birkaç saniyeye sığdırır.

Aynı islemlerin çıkarma için de sagladıgını söylememize gerek yok sanırım. Hatta daha da ileri gidip, bu oranların genisletilmis veya daraltılmıs hallerinde bile payların toplamını paydaların toplamına böldügümüzde orantı sabitinin adının hakkını vererek sabit kaldıgını söyleyebiliriz.

Yani;

esitligi inanılması zor olsa da gerçektir.

Orantı Çeşitleri

1. Doğru orantı:

Oranı sabit olan iki çokluk dogru orantılı veya kısaca orantılıdır denir.

Yani, çokluklardan biri artarken digeri de artıyorsa (ki ancak böyle oran sabit kalabilir) veya çokluklardan biri azalırken digeri de azalıyorsa, bu iki çokluk arasında dogru orantı vardır.

Örnegin, x ile y dogru orantılıysa

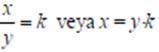
olmalıdır.

x, y, z sayıları sırasıyla a, b, c sayılarıyla orantılıysa

x gibi bir çokluk, bazen 1’den fazla çoklukla dogru orantılı olabilir. Mesela hem y hem de z ile dogru orantılı ise bunu da

yazarak gösteririz.

2. Ters orantı:

Çarpımları sabit olan iki çokluk ters orantılıdır veya aralarında ters orantı vardır denir.

Yani, çokluklardan biri artarken digeri azalıyorsa veya birisi azalırken digeri artıyorsa bir seylerin ters gittigini düsünür ve ters orantılılar deriz.

Örnegin, x ile y ters orantılı ise

olmalıdır.

x, y, z sayıları sırasıyla a, b, c sayılarıyla ters orantılıysa

deriz.

Bu eşitlikleri,

gibi düsünmek hiç de zor olmadıgından x, y, z sayılarının sırasıyla a, b, c sayılarıyla ters orantılı olmasının aslında (bilgi yelpazesi.net) sırasıyla

ile dogru orantılı oldugu sonucuna ulasırız.

Bazen bir deger, 1’den fazla degerle ters orantılı olabilir. Mesela x, hem y hem de z ile ters orantılıysa bunu

seklinde gösteririz.

3.Bileşik orantı

Bir orantının içinde hem dogru orantılı hem de ters orantılı olan çokluklar varsa böyle orantılara bilesik orantı denir.

Örnegin, bir x sayısı, y ile dogru ama z ile ters orantılıysa, bunu

seklinde gösteririz.

Aslında biraz önce çıkardıgımız sonucu kullanıp kendimizi ters orantıdan kurtarabiliriz.

Yani y ile dogru ama z ile ters orantılı olan x degerini hem y ile hem de

ile dogru orantılıymıs gibi düsünebiliriz. Bu da bizi aynı sonuca götürür.

Ortalamalar

1. Aritmetik ortalama

(A). x₁, x₂, x₃, … , x_n

Reel sayılarının aritmetik ortalaması (ortası)

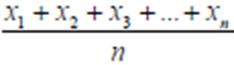
seklinde tanımlanır.

a ve b gibi iki reel sayının aritmetik ortası

olur.

2. Geometrik ortalama

(G). x₁, x₂, x₃, … , x_n

Pozitif reel sayılarının geometrik ortalaması (ortası)

seklinde tanımlanır.

Geometrik ortanın diger bir adı ise orta orantıdır.

a ve b gibi iki pozitif reel

sayının orta orantısı  olur.

3. Harmonik ortalama

(H). Sıfırdan farklı x₁, x₂, x₃, … , x_n reel sayılarının harmonik ortalaması (ortası)

seklinde tanımlanır.

a ve b gibi sıfırdan farklı iki reel sayının harmonik ortası

olur.

Uyarı 1. Ortalamaları bulunmak istenen pozitif reel sayıların tümü birbirlerine esit ve k ise tüm ortalamaları da birbirine esit ve k olur.

Uyarı 2. Eger bu pozitif reel sayıların sadece bir tanesi bile digerlerinden farklıysa H < G < A esitsizlikleri geçerli olur. Yani ortalamaların esitligi sadece sayıların tümünün birbirlerine esitligi ile mümkündür.

Uyarı 3. a ve b gibi sadece iki pozitif reel sayı için her zaman G² = AH’dır.

Teorem. a ve c gibi farklı iki reel sayının harmonik ortası H, geometrik ortası G, aritmetik ortası A, karesel ortası K ile simgelensin. Daima H < G < A < K’dır.

Kanıt: c > a olmak üzere üst tabanı a, alt tabanı c olan bir ABCD yamugunda tabanlara paralel olacak sekilde bir [PQ] çizelim

Sonuç olarak; eger [PQ] kösegenlerin kesisim noktasından geçiyor ise uzunlugu taban uzunluklarının harmonik ortası (H), olusan iki yamugu benzer yapıyor ise geometrik ortası (G), orta taban ise aritmetik ortası (A) ve olusan iki yamugun alanları denk yapıyor ise karesel ortası (K) oldugunu kanıtlamıs olduk.

Simdi de bu [PQ] dogru parçalarının yukarıdaki sırada giderek boylarının uzadıgını kanıtlamalıyız.

H < G’dir çünkü H  G oldugunda yamuklar benzer olmuyor. G < A’dır, çünkü G yamukları benzer yapıyor, üstteki yamuk alttaki yamuktan küçük oldugundan yüksekligi de küçük olmalı fakat G A olursa üst yamugun yüksekligi alttakinin yüksekliginden büyük veya esit olur. A<K dır, çünkü K yamukların alanlarını esit yapıyor, A  K olsaydı alttaki yamugun alanının üsttekinden daha büyük olacagı asikar.

Böylelikle H < G < A < K esitsizligini geometrik olarak kanıtlamıs olduk.

Bu arada a = c olursa H = G = A = K olur. Çünkü a = c durumunda yamuk paralelkenara dönüsür. Bir paralelkenarda orta taban hem tabanlara paraleldir, hem kösegenlerin kesisim noktasından geçer, hem alt ve üst paralelkenarları benzer yapar, hem de alt ve üst paralelkenarların alanlarını denk yapar. Gösterdigimiz bu dört ortalamadan baksa ortalamaların da sıralamadaki yerleri yamukta gösterdigimiz bu metot ile gösterilebiliyor. Fakat onları bu geometri notlarında göstermeyecegiz.