Eğitim Öğretim İle İlgili Belgeler > Konu Anlatımlı Dersler > Matematik Dersi İle İlgili Konu Anlatımlar

AÇI KENAR BAĞINTILARI (MATEMATİK KONU ANLATIM)

A,B, C dogrusal olmayan üç nokta oldugunda, [AB], [AC] ve [BC]’nin birlesimine ABC üçgeni denir.

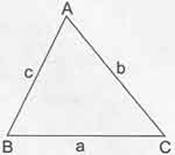
Üçgende Açı Kenar Bağıntıları

• Bir üçgende herhangi bir kenarın uzunluğu , diğer iki kenarın toplamından küçük, farkının mutlak değerinden ise büyüktür. Aşağıda bu açı kenar bağıntıları ile ilgili formül yer almaktadır.

|b-c| < a < b + c

|a-c| < b < a + c

|a-b| < c < a + b

Daha iyi anlamamız açısından bir örnek verelim.

Örnek: Yukarıdaki ABC üçgenine göre |AB|=4, |AC|=8 ise |BC| uzunluğunun alabileceği değerleri nelerdir?

Çözüm: |BC| uzunluğu yani a kenarı bizden isteniyor. Yukarıdaki formüle göre:

8-4<a<8+4 => 4<a<12 sonucu çıkar. Bunun da anlamı a’nın alabileceği değerler 5,6,7,8,9,10,11 değerleridir.

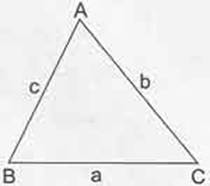
• Bir üçgende büyük açı karşısında büyük kenar, küçük açı karşısında küçük kenar bulunur.

Bir üçgende kenarlar arasında eşitlik var ise açılar arasında da eşitlik vardır.

• Üçgende açı kenar bağıntıları konusunda bir diğer önemli nokta da geniş açı ve dar açı şartlarıdır.

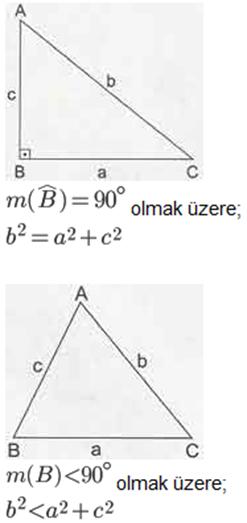
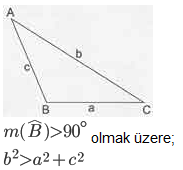
• Geometri dersinin bu konusunda bir diğer özellik de çeşitkenar üçgenle ilgilidir. Çeşitkenar bir ABC üçgeninde A köşesinden çizilen yükselik, açıortay ve kenarortay arasında bir bağıntı oluşmaktadır. Bu bağıntı şu şekildedir:

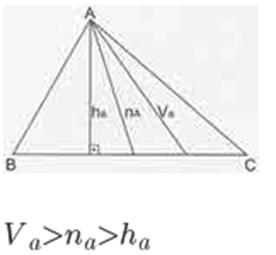
• Bir üçgenin iç açıları arasındaki sıralama ile yardımcı elemanları arasındaki sıralama terstir.

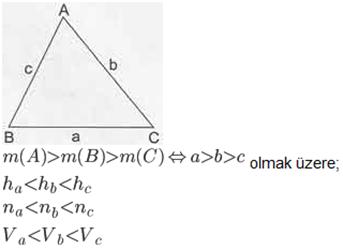
Örnekler:

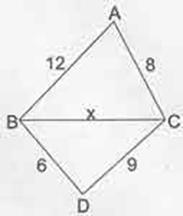
Örnek: ABCD bir dörtgen olmak üzere;

|AB|=12, |AC|=8, |BD|=6, |DC|=9 olduğuna göre |BC|= x’in alabileceği tam sayı değerleri kaç tanedir?

Çözüm: ABC üçgeninde; 12-8<x<12+8 => 4<x<20

BCD üçgeninde; 9-6<x<9+6 => 3<x<15

Bu iki üçgenin sonucunu (bilgi yelpazesi. com) ortak çözersek

4<x<15 olacağından x’in alabileceği değerler 10 tane olacaktır.

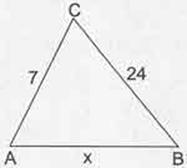
Örnek: ABC bir üçgen, |AC|=7, |CB|=24 olmak üzere;

Yandaki şekilde C açısı geniş açı olduğuna göre |AB|=x’in alabileceği en küçük tam sayı değeri kaçtır?

Çözüm: Üçgen eşitsizliğinden;

24-7<x<24+7 burdan 17<x<31 sonucu çıkar.

Geniş açı sorulduğundan m(C)>90º olduğuna göre;

x²>7²+24²

x>25 => 25<x<31 olacağından x’in alabileceği en küçük tam sayı değeri 26 olacaktır.