Eğitim Öğretim İle İlgili Belgeler > Konu Anlatımlı Dersler > Matematik Dersi İle İlgili Konu Anlatımlar

KESİR PROBLEMLERİ (MATEMATİK DERSİ İLE İLGİLİ KONU ANLATIMLAR)

Örnek 1

Ahmet parasının  ini harcadığında geriye 80 000 lirası kalıyor.

Ahmet’in başlangıçta kaç lirası vardı?

A) 120 000             B) 150 000             C) 180 000             D) 200 000

Çözüm

1. Yol:

Parasının  ini harcadığına göre, parasının tamamı

80 000 ise, 80®2 birim  000 : 2 = 40 000 (1 birim)

Tamamı= 40 000 x 5 = 200 000 liradır.

Ill. Yol:

Parasının tamamı x lira olsun:

Cevap D

Örnek 2

İbrahim parasının  unu Şerife’ye verdiğinde; Şerife’nin parası, kendi parasının  i oranında artıyor.

Buna (bilgi yelpazesi.net) göre, İbrahim’in parasının Şerife’nin parasına oranı kaçtır?

A) 3                    B) 4                    C) 8                    D) 12

Çözüm

İbrahim’in parası: x TL

Şerife’nin parası: y TL olsun.

Verilenlere göre,

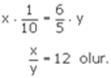
Cevap D

Örnek 3

Bir sayının

inin toplamı aynı sayının

inin toplamından 13 fazladır. Buna göre, bu sayı kaçtır?

A) 35                    B) 50                    C) 60                    D) 70

Çözüm

İstenen sayı x olsun. Verilenlere göre,

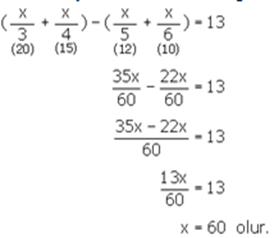
Cevap C

Örnek 4

Bir kesrin değeri  tir. Bu kesrin paydasından 5 çıkarılır, payına 5 eklenirse kesrin değeri oluyor.

Buna göre, ilk kesrin payı kaçtır?

A) 2                    B) 3                    C) 4                    D) 5

Çözüm

Örnek 5

Bir bidonun kütlesi boş iken x gram, üçte biri su ile dolu iken y gramdır.

Bu bidonun tamamı su ile dolu iken, toplam kütle kaç gramdır?

A) 2x – 3y                    B) 2x + 3y                    C) 3y – 2x                    D) 3x – 4y

Çözüm

Boş bidonun kütlesi: x gram

Bidonun tamamını (bilgi yelpazesi.net) dolduran suyun kütlesi: s gram olsun.

Üçte biri su ile dolu iken bidonun kütlesi: y gram olduğuna göre,

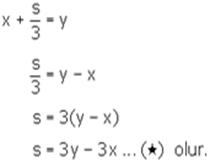
Boş bidonun kütlesi: x gram ve bidonun tamamını dolduran suyun kütlesi: 3y – 3x gram olduğuna göre, tamamı su ile dolu bidonun kütlesi:

Cevap C

Örnek 6

Ayşe’nin parasının  si 200 000 lira ise, tamamı kaç liradır?

A) 650 000                  B) 700 000                  C) 780 000                  D) 800 000

Çözüm

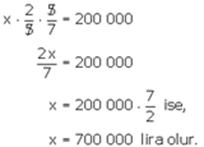
Cevap B

Örnek 7

Bir sayının  inin 10 fazlası, aynı sayının 14 eksiğine eşittir. Buna göre, bu sayı kaçtır?

A) 30                    B) 32                    C) 35                    D) 45

Çözüm

Cevap A

Örnek 8

Bir havuzun yarısı su ile doludur. Bu havuza 20 litre daha su ilave edilirse havuzun  ü doluyor. Havuzun tamamı kaç litreliktir?

A) 56                    B) 64                    C) 70                    D) 80

Çözüm

Cevap D

KESİRLER, RASYONEL SAYILAR, ÇEŞİTLERİ, ÖZELLİKLERİ, KESİR PROBLEMLERİ (MATEMATİK DERSİ İLE İLGİLİ KONU ANLATIMLAR)

Tanım:

a, b e Z ve b ¹ 0 olmak üzere

  biçiminde yazılabilen sayılara rasyonel sayı denir ve Q ile gösterilir.

a ya rasyonel sayının payı,  b ye ise paydası adı verilir.

Örnek

a)  BASİT KESİR

Payı paydasından küçük olan kesire (işaretine bakılmaksızın) basit kesir denir.

kesrinde lal < lbl dır.

Örnek

b)  BİLEŞİK KESİR

İşaretine bakılmaksızın payı paydasından büyük veya payı paydasına eşit olan kesirlere bileşik kesir denir.

kesrinde |a| ³ |b| dir.

Örnek

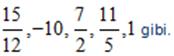
c)  TAMSAYILI KESİR

Sıfır hariç bir tam sayı ve basit kesir ile birlikte yazılan kesir sayılarına tam sayılı kesir denir.

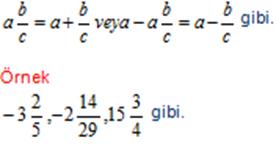
RASYONEL SAYILARDA DÖRT İŞLEM

1) Toplama - Çıkarma

Öncelikle paydalar eşit değil ise eşitlenir. Sonra paylar arasında işlem yapılır. Payda ortak olarak aynen yazılır.

2. Çarpma

Paylar çarpılıp paya, paydalar çarpılıp paydaya yazılır.

3. Bölme

Birinci kesir aynen yazılır, ikinci kesir ters çevrilip çarpma işlemi yapılır.

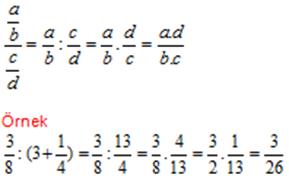
MERDİVENLİ İŞLEMLER

Merdivenli kesirlerde önce ana kesir çizgisi belirlenir. En üst ve en alt noktalardan ana kesir çizgisine yaklaşarak işlem (bilgi yelpazesi.net) yapılır.

Örnek

RASYONEL SAYILARDA SIRALAMA

Aşağıdaki yöntemler pozitif rasyonel sayılarda sıralama için geçerlidir, negatif rasyonel sayılar sıralanırken önce pozitifmiş gibi sıralanıp sonra yön değiştirir.

1) Eşitleme Metodu

a)  Paylar eşitlenirse paydası küçük olan kesir daha büyüktür.

Örnek

b) Paydalar eşitlenirse payı büyük olan kesir daha büyüktür.

Örnek

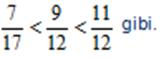
2. Fark Metodu

Pay ile payda arasındaki fark eşit ise;

a)  Basit kesirlerde payı küçük olan kesir daha küçüktür.

b) Bileşik kesirlerde payı küçük olan kesir daha büyüktür.

Örnek

3. Ondalık Sayıya Çevirme Metodu:

Rasyonel sayılar, ondalık sayıya çevrilip sonra sıralama yapılabilir.

a, b, c yi sıralayınız.

Çözüm

ARADA OLMA

İki rasyonel sayı arasında çok sayıda (sınırsız sayıda) rasyonel sayı vardır. Ancak bu sayılar sayı eksenini tamamen doldurmaz. Çünkü sayı doğrusunda görüntüsü olduğu halde rasyonel olmayan sayılar vardır. İçin

x yerine 25, 26, 27 olmak üzere 3 tane doğal sayı yazılabilir.

ONDALIK SAYILAR

Tanım:

Paydası 10 un kuvvetleri biçiminde olan (veya bu şekle getirilebilen) kesirlere ondalık kesir denir. Bir ondalık kesrin virgülden (bilgi yelpazesi.net) önceki kısmına tam kısmı, virgülden sonraki kısmına kesir kısmı denir.

Ondalık Kesirlerde Çözümleme

Bir ondalık kesri basamak değerlerinin toplamı biçiminde ifade etmeye ondalık kesri çözümleme denir.

Örnek

43,527 sayısını çözümleyelim:

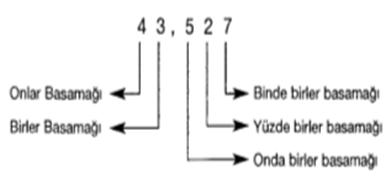
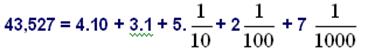
şeklinde çözümlenir.

Bir ondalık kesrin, kesir kısmının sonuna yazılacak sıfırlar bu ondalık kesrin değerini değiştirmez.

Örnek

5,28 = 5,280 = 5,2800 ... gibi.

ONDALIK SAYILARDA DÖRT İŞLEM

1) Toplama-Çıkarma:

Virgüller alt alta gelecek biçimde yazılır ve işlem yapılır. Sonuç aynı basamaktan (hizadan) virgülle ayrılır.

Örnek

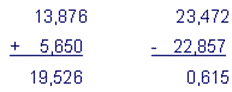
gibi.

2) Çarpma:

Virgül yokmuş gibi işlem yapılır. Sonuç; her iki çarpanın virgülden sonraki kısımlarının basamak sayısının toplamı kadar sağdan sola doğru virgülle ayrılır.

Örnek

3) Bölme

Pay ve paydadaki sayılar virgülden kurtarılır. Yani 10 un katları ile genişletilip sadeleştirilir.

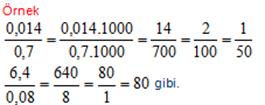
DEVİRLİ ONDALIK SAYI

Ondalık biçimde yazılan bir rasyonel sayının ondalık kısmındaki rakamlar belli bir biçimde tekrarlanıyor ise bu sayıya devirli ondalık sayı denir ve devreden kısmın üzerine (-) işareti konur.

Örnek

Her rasyonel sayı devirli bir ondalık sayı biçiminde, her devirli ondalık sayı rasyonel sayı biçiminde yazılabilir.

Devirli Sayının Rasyonel Sayı Biçiminde Yazılması

Devirli bir ondalık sayıyı rasyonel sayıya şu şekilde çeviririz.

Örnek

2.