eğitim öğretim ile ilgili belgeler > konu anlatımlı dersler > matematik dersi ile ilgili konu anlatımlar

LOGARİTMA, LOGARİTMA ÇEŞİTLERİ, LOGARİTMA ÖZELLİKLERİ İLE İLGİLİ KONU ANLATIMLAR (MATEMATİK DERSİ İLE İLGİLİ KONU ANLATIMLAR, ÖRNEKLER, ÇÖZÜMLÜ SORULAR)

 

1. TANIM

 

aR⁺ -{1} ve  x R⁺ olmak üzere, a^y = x eşitliğini ele alırsak.

Bu eşitlikte; a değerini bulmak için kök alma, x değerini bulmak için kuvvet (üs) alma , y değerini bulmak içinde logaritma işlemi yapılır.

aR⁺-{1}, xR⁺ ve yR olmak üzere,

 

ay=x Û y=log_a x    tir.

 

Burada; y sayısı , x sayısının a tabanına göre logaritmasıdır.

 

Örnekler:

1) log₂ 8 = y Þ 8= 2^y Þ y = 3 tür.

2) log_a 64 = 3 Þ 64 = a³ Þ a = 4 tür.

4) log_a a = x Þ a = a^x Þ x = 1 dir.

5) log_a 1 = n Þ 1 = aⁿ Þ n = 0 dır.

6) log₅ (-25) v= m Þ -25 = 5^m Þ mR dir.

 

Sonuç olarak:

1) log_a a = 1

2) log_a 1 = 0

3)y = log_a f(x) Þ f(x) > 0

 

Örnek:

Log₅ (log₃ (log₂ x) ) = 0 olduğuna göre, x değerini bulalım.

 

Çözüm:

Log₅ (log₃ (log₂ x) ) = 0 Þ log₃ (log₂ x ) = 5⁰ = 1 Þ log₂ x = 3¹ Þ x = 2³ = 8 dir.

 

Örnek:

Log₃ (a³.b.c) = 5

olduğuna göre, a.b çarpımını bulalım.

 

Çözüm:

log₃(a³.b.c) = 5 Þ  a3.b.c = 3⁵

 

 

Örnek:

Buradan, a.b = 18 dir.

 

2. ÖZEL LOGARİTMALAR

 

a) Bayağı Logaritma

y = log₁₀ x = log x fonksiyonuna 10 tabanında logaritma veya bayağı logaritma denir.

 

Örnek:

log₁₀ 10 = log10 = 1 dir.

 

b) Doğal Logaritma

e = 2,71828…. olmak üzere,

y = log_e x = ln x fonksiyonuna doğal logaritma denir.

 

Örnek:

Log_e e = ln e = 1 dir.

 

 

3. LOGARİTMANIN ÖZELLİKLERİ

 

x,yR⁺ ve a R⁺ - {1} olmak üzere,

 

1) log_a (x.y) = log_a x + log_a y

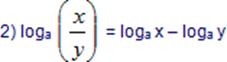
4) log_a x = log_a y Þ x = y      dir.

 

 

Örnek:

1) log 5 + log 2 = log (5.2) = log 10 =1

 

Örnek:

log (2x-y) = log x + log y  olduğuna göre, y nin x türünden eşitini bulalım.

 

Çözüm:

log (2x-y) = log x + log y Þ log (2x-y) = log (x.y)

Þ 2x – y = x.y

Þ 2x = x.y +y

Þ 2x = y. (x+1)

 

Örnek:

 

log 5 = a,  log 3 = b, log 2 = c    olduğuna göre, log (22,5) ifadesinin a,b,c türünden eşitini bulalım.

 

 

Çözüm:

 

= a + 2b – c  dir.

 

Þ 2. log₅ x = 6 – log₅ x

Þ 3. log₅ x = 6

Þ log₅ x = 2

Þ x = 5² = 25   tir.

 

Örnek:

 

log 5 = n         olduğuna göre, log 4 değerinin n türünden eşitini bulalım. bilgi yelpazesi.net

 

Çözüm:

 

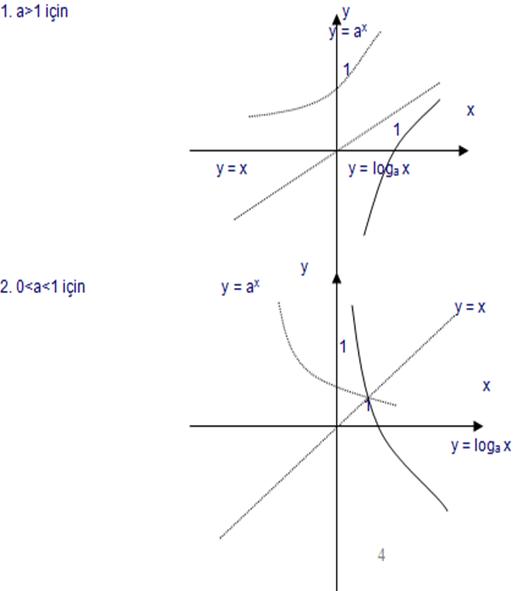
aR⁺, a1 ve xR⁺ olmak üzere,

 

 

Örnek:

log₂5 =       olduğuna göre, log₅10 ifadesinin  türünden eşitini bulalım.

 

Çözüm:

 

 

 

4. LOGARİTMA FONKSİYONUNUN GRAFİĞİ

 

Üstel fonksiyon bire bir ve örten olduğu için ters fonksiyonu vardır ve bu fonksiyona logaritma fonksiyonu denir.

 

 

Y = log_a x fonksiyonunun grafiği a nın durumuna göre çizilirse,

 

grafikleri elde edilir.

 

 

Not:

 

y = log_a (mx + n)fonksiyonunun grafiği, aşağıdaki işlemler yapılarak çizilir.

1) Logaritmanın tanımından,   f(x) in grafiği, mx + n > 0 şartının sağlandığı bölgededir.

2) y = 0 ve y = 1 için sırasıyla x₀ ve x₁ değerleri bulunur. Grafik, (x₀,0) ve (x₁,1) noktalarından geçer.

 

 

Örnek:

f(x) = log₂ (x-1) fonksiyonunun grafiğini çizelim.

 

Çözüm:

f(x) fonksiyonu, x-1>0 Þ  x>1 için tanımlıdır.

y = 0 için, log₂ (x-1) = 0  Þ x = 2 ve

y = 1 için, log2 (x-1) = 1 Þ x = 3

olduğundan grafik (2,0) ve (3,1) noktalarından geçer. Taban 1 den büyük olduğundan, verilen fonksiyonun grafiği,

 

 

5. LOGARİTMA FONKSİYONUNUN TERSİ

aR⁺-{1} ve xR⁺ olmak üzere,

f(x) = log_a x Û f ^-1 (x) = a^x      tir.

 

Örnek:

 

f(x) = log₅x Û f ^–1 (x) = 5^x tir.

 

Örnek:

f(x) = y = 2log₅ x Þ x = 2.log₅ f ^–1 (x)

 

 

6. LOGARİTMALI EŞİTSİZLİKLER

 

Bir eşitsizlik içinde bilinmeyenin logaritması varsa bu tür eşitsizliklere logaritmalı eşitsizlikler denir.

 

1) a>1 olmak üzere,

log_a f(x) log_a g(x) Û f(x)  g(x)   (eşitsizliğin yönü değiştirilmez.)

2) 0<a<1 olmak üzere,

log_a f(x) log_a g(x) Û f(x) g(x)      (eşitsizliğin yönü değiştirilir.)

 

Örnek:

log₃ (log₂(x-1)) > 0 Þ log₂ (x-1) > 3⁰ = 1

Þ x-1 > 2¹

Þ x > 3 tür.

 

Örnek:

log₂(x-3)<4 Þ 0 < x-3 <2⁴

Þ 3<x<19 dur.

 

Örnek:

 

7. BAYAĞI LOGARİTMA

 

a) Karekteristik ve Mantis

 

xR+ , kZ ve 0m<1 olmak üzere, log x = k+m eşitliğinde k tamsayısına x in logaritmasının karekteristiği, m reel sayısına da  x in logaritmasının mantisi denir. bilgi yelpazesi.net

 

Örnek:

 

log 30 = 1,477 ifadesinde, 30 sayısının logaritmasının karekteristiği1 ve mantisi 0,477 dir.

 

Örnek:

 

log2 = 0,301   olduğuna göre, log(800) değerinin karekteristik ve mantisini bulalım.

 

Çözüm:

 

log (800) = log (2³.10²) = 2 + 3 log2

= 2 + 3. (0,301)

= 2 + 0,903

= 2,903 olduğundan,

karekteristik 2 ve mantis 0,903 olur.

 

Not:

 

 

Uyarı:

 

1 den büyük pozitif tamsayıların basamak sayısı, sayının logaritmasının karekteristiğinin bir fazlasıdır.

 

Örnek:

 

log 2 = 0,301 olduğuna göre, (40)⁴⁰ sayısının kaç basamaklı bir sayı olduğunu bulalım.

 

Çözüm:

Log (40)⁴⁰ = 40. log(40)

= 40. (log 2².10)

= 40. (1 + 2 log 2)

= 40. (1+ 0,602)

= 64,08 olduğundan, karekteristik 64 ve basamak sayısı 65 tir.

 

b) Kologaritma:

 

xR⁺ olmak üzere, x in çarpmaya göre tersinin logaritmasına x in kologaritması denir ve colog x biçiminde gösterilir.

 

tir.

 

Örnek:

 

log x = 1,73     olduğuna göre, colog x in karekteristiğini ve mantisini bulalım.

 

 

“MATEMATİK DERSİ İLE İLGİLİ KONU ANLATIMLAR” SAYFASINA GERİ DÖNMEK İÇİN

>>>TIKLAYIN<<<

“MATEMATİK DERSİ İLE İLGİLİ TEST SORULARI, SORU BANKASI” SAYFASINI GÖRMEK İSTERSENİZ

>>>TIKLAYIN<<<

“MATEMATİK DERSİ İLE İLGİLİ YAZILI SORULARI” SAYFASINI GÖRMEK İSTERSENİZ

>>>TIKLAYIN<<<