Eğitim Öğretim İle İlgili Belgeler > Konu Anlatımlı Dersler > Matematik Dersi İle İlgili Konu Anlatımlar

PERMÜTASYON, PERMÜTASYON ÇEŞİTLERİ, PERMÜTASYON ÖZELLİKLERİ (MATEMATİK DERSİ İLE İLGİLİ KONU ANLATIMLAR, ÖRNEKLER, ÇÖZÜMLÜ SORULAR)

n elemanlı bir kümenin elemanlarını bir sırada yazmaya onun bir Permütasyonu denir.

Örneğin üç elemanlı bir a,b,c kümesinde  bir permütasyon (a, c, b) başka bir permütasyondur.

Permütasyonların Sayısı

n elemanlı bir kümenin elemanlarının pemü-tasyonlarının sayısı P(n, n) biçiminde gösterilir.

Değeri P(n, n) = n! dir.

(çarpma kuralı ile bulunduğuna dikkat ediniz.)

n elemanlı bir kümenin r elemanlı alt kümelerinin permütasyonlarının sayısı P(n, r) ile gösterilir. P(n,r) yi hesaplıyalım.

n elemanlı kümenin r elemanlı bir alt kümesinde r tane eleman vardır. Bunların yerlerine kaç tane eleman yazılabileceğini altına yazalım ve çarpma kuralını uygulayalım.

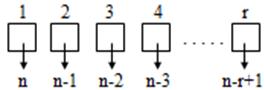
o halde

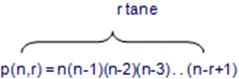
çarpımıdır.

Bunu basitleştirmek için paydayı 1 kabul edip pay ve paydayı (n-r)! İle çarpalım,

buna göre,

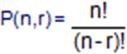
formülü bulunur.

PERMÜTASYONLA İLGİLİ ÖRNEK PROBLEMLER, SORULAR

ÖRNEK:

Ankara’da arabalara üç harf ve 2 rakam kullanılarak plaka verilmektedir. (kullanılan harf sayısı 25 ve aynı harf birden fazla kullanılmaktadır.) Buna göre kaç arabaya plaka verilebilir.

ÇÖZÜM:

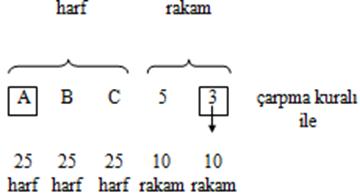
S = 25.25.25.10.10 = 1562500 arabaya plaka verilir.

ÖRNEK:

Bir erkek öğrencinin 2 çift ayakkabısı, 2 ceket, 4 pantolon 3 gömleği ve üç değişik kravatı bulunmaktadır. Bunları kullanarak (hergün bir şeyi farklı olarak) giyinecektir. Kaç gün değişik kıyafetle çıkabilir ?

ÇÖZÜM:

Çarpma kuralı gereği bu değişik şeylerin çarpımı kadar gün değişik kıyafet giyer.

2.2.4.3.3 = 144 gün

ÖRNEK:

Bir otomobilde 5 kişilik yer vardır. (sürücü yeri dahil) 2 sinin sürücü belgesi bulunan beş kişi bu otomobilde kaç değişik biçimde seyahat edebilir ?

ÇÖZÜM:

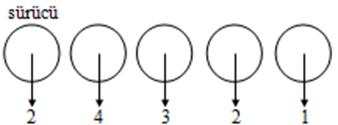
sürücü yerine 2 değişik kişi oturabilir. Diğer yerlere sıra ile 4, 3, 2, 1 değişik kişi oturabilir. O halde çarpma kuralı gereği 2.4! = 48 değişik biçimde oturabilirler.

ÖRNEK:

 kümesinin elemanları ile üç basamaklı, rakamları tekrarsız kaç sayı yazılabilir.

ÇÖZÜM:

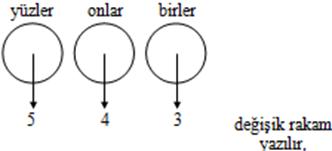
çarpma kuralı gereğince 5.4.3 = 60 sayı yazılabilir.

ÖRNEK:

MERSİN kelimesindeki 6 harfle anlamlı yada anlamsız kaç sözcük yazılabilir ?

ÇÖZÜM:

P(6, 6) = 6! Kadar sözcük yazılabilir.

n elemandan (a) tanesi aynı ise bunların permütasyonlarının sayısı

ÖRNEK:

SİVAS kelimesindeki harflerle anlamlı yada anlamsız 6 harfli kaç sözcük yazılabilir.

ÇÖZÜM:

S harfi iki kez olduğu için bu ikisi aynıdır. O halde

n elemandan bazıları aynı ise örneğin n1 tanesi aynı n2 tanesi de başka aynı ise bunlarla n elemanın permütasyonlarının (bilgi yelpazesi.net) sayısı    dir.

ÖRNEK:

MARMARA kelimesindeki harflerle 7 harfli anlamlı yada anlamsız kaç sözcük yazılabilir ?

ÇÖZÜM:

MARMARA kelimesindeki harflerden 2 tanesi M, üç tanesi A ve iki tanesi de R dir.

O halde,

sözcük yazılabilir.

ÖRNEK:

4 tane 2 rakamı, 2 tane 5 rakamı ve diğerleri 4, 6 rakamları olan 8 rakamları olan 8 rakamla kaç değişik sekiz basamaklı sayı yazılabilir ?

ÇÖZÜM:

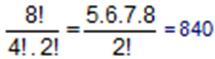
tane sekiz basamaklı değişik sayı yazılabilir.

ÖRNEK:

5 arkadaştan ikisi kızdır. Bunlar 5 kişilik bir bankta oturmak istiyorlar. İki kız daima yan yana oturmak koşulu ile bu banka kaç değişik biçimde oturabilirler ?

ÇÖZÜM:

Kız öğrenciler A ve B ise (A, B) yi, bir kişi gibi düşünürsek 4 kişi gibi olur ve 4! Kadar otururlar. Ancak (A, B) de (A, B) ve (B, A) gibi iki değişik hal vardır. Çarpma kuralı gereğince; 2! . 4! = 2.24 = 48 değişik biçimde otururlar.

ÖRNEK:

5 arkadaştan ikisi küstür. 5 kişilik bir bankta oturmak istiyorlar. İki küs arkadaş yan yana gelmemek koşulu ile kaç değişik biçimde otururlar ?

ÇÖZÜM:

Önce iki kişi yan yana olmak koşulu ile oturabilme bulunur. Bu sayı 2!4! dir. (bir önceki problemi inceleyiniz) 5 öğrenci bu banka 5! değişik biçimde otururlar. Bu sayıdan yan yana oturma sayısını çıkarırsak; yan yana aturmama sayısı bulunur.

5! – 2!4! = 120 – 48 = 72 değişik biçimde otururlar.

ÖRNEK:

(3, 3, 3, 2, 2, 4, 4, 4) rakamları ile 8 basamaklı kaç değişik sayı yazılabilir ?

ÇÖZÜM:

Üç tane 3, iki tane 2 ve üç tane 4 olduğu için

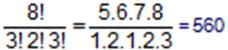
değişik sayı yazılabilir.

ÖRNEK:

Beş değişik oyuncak 3 çocuğa kaç değişik biçimde dağıtılabilir ?

ÇÖZÜM:

Oyuncalar değişik olduğu için bu bir sıralama problemi ve permütasyondur. 5 elemanın üçlü permütasyonudur. O halde

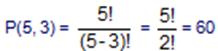
değişik biçimde dağıtılabilir.

ÖRNEK:

6 kitap, kitaplıkta bir rafa kaç değişik biçimde sıralanabilir ?

ÇÖZÜM:

Altının altılı permütasyonu kadar sıraya konulabilir. P(6, 6) = 6! = 720 değişik sırada yerleştirilebilir.

ÖRNEK:

Bir öğrencinin 3 matematik, 2 fizik ve 4 türkçe kitabı vardır. Her branştaki kitaplar yan yana gelmek koşulu ile bir rafa kaç değişik biçimde yerleştirilebilir ?

ÇÖZÜM:

Matematik kitapları 3!, fizik kitapları 2! ve Türkçe kitapları 4! Kadar sıraya konur. Ancak bunlar Matematik, Fizik ve Türkçe (bilgi yelpazesi.net) olmak üzere üç branştır. Bunlar da kendi arasında 3! kadar sıraya konabilir. Yani (M, F, T) yada (M, T, F) gibi değişik 3! sırada dizilebilir.

O halde çarpma kuralı gereği 3!2!4! . 3! = 6.2.24.6 = 1728 değişik biçimde yerleştirilebilir ?

ÖRNEK:

6 arkadaş sinemaya gitti. Boş olan 4 tane numaralı sandalye ye kaç değişik biçimde oturabilirler ?

ÇÖZÜM:

Yerler  değişik  numarada  olduğu için permütasyondur.(sıra önemli) O halde

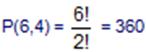
bulunur.

ÖRNEK:

İki torbanın her birinde, üzerlerinde 1 den 12 ye kadar numara bulunan bilyeleri vardır. Her birinden 1 bilye alınarak ikili gruplar elde ediliyor. Kaç değişik ikili elde edebilirsiniz. ?

ÇÖZÜM:

Her  birinde  değişik  12 şer  bilye olduğu için bunların çarpımı kadar değişik ikili elde edilir.

12.12 = 144 (değişik ikili)

ÖRNEK:

6 kişiden ikisi önde 4 ü arkada olmak üzere sıralanarak fotoğraf çektirilecektir. Kaç poz resim çekilebilir.

ÇÖZÜM:

Önde

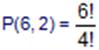
arkadakiler = P(4, 4) = 4! dir. O halde

poz bulunur. (hepsinin aynı sırada olmasının sonucu değiştirmeyeceğine dikkat ediniz.)

ÖRNEK:

P(n, 4) = 42.P(n, 2) ise n kaçtır. P (n, r) n elemanlı r li permütasyonların sayısıdır.

ÇÖZÜM:

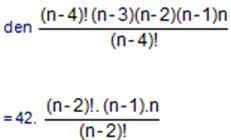
sadeleşme yapılarak (n-2) . (n-3) = 42 bulunur.

O halde

n² – 5n + 6 – 42 = 0

n² – 5n – 36 = 0

(n-9)(n+4) = 0  n = 9 ; n = -4

(n= -4) olamaz. O halde n = 9 dur.

ÖRNEK:

  kümesinin elemanları ile yazılabilen  5 rakamlı sayılardan kaç tanesinde 2 rakamı vardır.

ÇÖZÜM:

2 rakamı hepsinde bulunacağı için 2 yi ayrı tutarsak geriye kalan 5 elemanın 4 lü permütasyonları kadar (2 hariç) dört rakamlı sayı yazılabilir. 2 sayısı bu 4 rakamlı sayıda 5 değişik   yerde  olabileceği  için  çarpma yöntemi gereği

sayı bulunur.

ÖRNEK:

10 kişi üzeri numaralı 8 sandalyeye kaç değişik şekilde oturabilir

ÇÖZÜM:

kadar değişik biçimde oturabilir.

DAİRESEL PERMÜTASYON

Bir kümenin elemanlarını bir dairenin çevresi etrafında sıralamaya dairesel permütasyon yada dönel sıralama denir. (Dairesel permü-tasyonlarda bir elemanın bulunduğu yer önemli değil sadece sağında ve solunda bulunan elemanlar önemlidir.) n elemanın Dairesel permütasyonların sayısı:

(n-1)! dir.

ÖRNEK:

Beş kişi yuvarlak bir masa etrafına kaç değişik biçimde oturabilir ?

ÇÖZÜM:

Dairesel permütasyon olduğu için

(5-1)! = 4! = 24 değişik biçimde oturabilirler.

ÖRNEK:

3 erkek, 2 kız arkadaş yuvarlak bir masa etrafına iki kız daima yan yana oturmak koşuluyla kaç değişik biçimde oturabilir ?

ÇÖZÜM:

A ve B kızlar ise (A, B) yi bir eleman olarak alırsak artık 4 kişi olur ve 3! kadar otururlar. Ancak iki kız (A, B) biçiminde olduğu gibi (B, A) biçiminde de alınabilir.

Çarpma kuralı ile bulunur.

2! . 3! = 12 değişik biçimde oturabilirler.

ÖRNEK:

7 arkadaştan belli iki kişi yan yana gelmemek koşulu ile daire biçiminde bir masa etrafına kaç değişik biçimde oturabilirler ?

ÇÖZÜM:

Önce tüm oturabilme sayısı  bulunur. Sonra belli iki kişinin yan yana gelme sayısı bulunur.

Bunlar birbirinden çıkarılınca yan yana gelmeme sayısı bulunmuş olur.

Tüm oturma sayısı (7-1)! = 6! = 720; belli ikisi yan yana oturma sayısı

2! (6-1)! = 2.5! = 2.120 = 240 istenilen belli iki kişinin yan yana oturmama sayısı ise:

720 – 240 = 480 bulunur.

ÖRNEK:

Daire şeklinde bir masa da 4 çocuk ve 4 bayan daima iki bayan arasında 1 çocuk bulunmak koşulu ile kaç değişik biçimde oturabilirler ?

ÇÖZÜM:

Önce  4  çocuğu birer atlayarak 4ün dairesel permütasyonu  kadar yönü

(4-1)! = 3! = 6 değişik biçimde otururlar. Araya bayanları oturtacağımız için bunların sayısı normal permütasyondur. 4! = 24 olur.

Çarpma kuralı gereği tüm sayı 3! 4! = 6 . 24 = 144 bulunur.

ANAHTARLIK PROBLEMLERİ

Anahtarlıklar havada döndürülebildiği için (pozitif yada negatif yön önemli değildir.) dairesel permütasyon sayısının yarısını almak (bilgi yelpazesi.net) gerekir. Ancak daire şeklindeki bir anahtarlığa maskot ilave edilmişse (anahtar maskotlu ise) normal permütasyon uygulanır ve yarısı alınır. (n>2 olmak üzere), (n) anahtar,maskotsuz anahtarlığa  ; mas-kotlu anahtarlığa   değişik biçimde takılabilir.

ÖRNEK:

5 değişik anahtar halka şeklinde maskotsuz bir anahtarlığı kaç değişik biçimde takılabilir ?

ÇÖZÜM:

bulunur.

ÖRNEK:

6 değişik anahtar halka şeklinde maskotlu bir anahtarlığa kaç değişik biçimde takılabilir ?

ÇÖZÜM:

değişik biçimde takılabilir.

ÖRNEK:

Bir çocuk değişik renkte ve büyüklükte 5 boncukla halka şeklinde bir kolye yapmak istiyor.(klips takmadan) Bu boncuklar kaç değişik biçimde yerleştirilebilir ?

ÇÖZÜM:

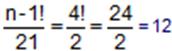
değişik biçim olur.

Not: Eğer klips taksydı diğer yanına geçemeseydi o zaman

değişik biçimde olurdu.