eğitim öğretim ile ilgili belgeler > konu anlatımlı dersler > matematik dersi ile ilgili konu anlatımlar

TRİGONOMETRİ, TRİGONOMETRİNİN ÖZELLİKLERİ, ÇEŞİTLERİ İLE İLGİLİ KONU ANLATIMLAR (MATEMATİK DERSİ İLE İLGİLİ KONU ANLATIMLAR, ÖRNEKLER, ÇÖZÜMLÜ SORULAR)

 

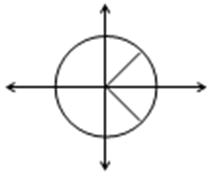
Yönlü Açı:

Saat yelkovanının dönme yönünün tersine pozitif yön, saat yelkovanının dönme yönüne de negatif  yön denir.

 

Açı Ölçü Birimleri:

 

Derece: Bir çemberin 360 da 1 ini gören merkez açının ölçüsü 1 derecedir.

1 derece  60 dakikadır. 1 dakika  60  saniyedir.

1^o = 60¢ ,  1¢= 60¢¢

 

Radyan: Bir çemberin, yarıçapının uzunluğundaki yayı gören merkez açı 1 radyandır.

 

Grad: Bir çemberin 400 de 1 ini gören merkez açının ölçüsü 1 grattır.

 

 

 

Esas Ölçü:

 

Derece cinsinden bir açının 360^o ye bölümünden kalan, derece cinsinden esas ölçü, radyan cinsinden bir açının 2p ye bölümünden kalan, radyan cinsinden esas ölçü adını alır.

 

 

Trigonometrik Fonksiyonlar:

Açının sinüsü ve kosinüsü:

Birim çember üzerinde, AOP açısını gözönüne alalım. P noktasının apsisine açının kosinüsü, ordinatına da açının sinüsü denir.

x₀ = cosa ,      y₀ = sina

Sonuç:

1.   P noktası çember üzerinde ve yarıçapı 1 birim olduğu için;

-1 £ cosa £ 1  veya  cos: R ® [-1,1]  dir.

 

Yani kosinüs fonksiyonunun tanım kümesi R, görüntü kümesi [-1,1] dir. Aynı şekilde;

 

-1 £ sina £ 1  veya  sin: R ® [-1,1]  dir.

 

Yani sinüs fonksiyonunun tanım kümesi R, görüntü kümesi [-1,1] dir.

 

2.   x₀ = cosa  ve  y₀ = sina  olduğuna göre;    cos²a + sin²a= 1 dir.

 

Açının tanjantı ve kotanjantı:

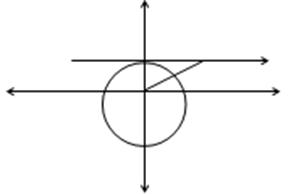
Birim çemberin A noktasındaki teğetini inceleyelim. Bu durumda t bir reel sayı olmak üzere, T(1,t) noktası teğetin üzerindedir. T noktasının ordinatına AOT açısının tanjantı denir. t = tana  dir.

 

Sonuç:

T(1,t) noktası teğet üzerindeki herhangi bir nokta için, t herhangi bir nokta olabilir. Dolayısıyla;

"a Î T={a ½aÎ IR ve a¹p/2 +kp, kÎ Z } için  tan: T ® R  dir.

Yani tanjant fonksiyonunun tanım kümesi (p/2 +kp) hariç bütün gerçel sayılar, görüntü kümesi R dir.

"a Î K={a ½aÎ IR ve a¹kp, kÎ Z } için  cot: K ® R  dir.

Yani tanjant fonksiyonunun tanım kümesi (kp) hariç bütün gerçel sayılar, görüntü kümesi R dir.

 

 

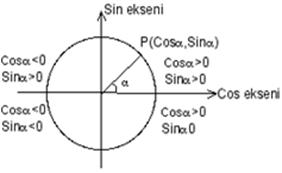
BİRİM ÇEMBER:

 

Merkezi orijinde olan ve yarıçapı 1 birim olan çemberdir.

 

 

x ekseni, Cosinüs ekseni

 

y ekseni , Sinüs eksenidir.

 

Analitik düzlemde trigonometrik fonksiyonların işaretleri

 

 

Periyodik Fonksiyonlar:

 

¦:A®B bir fonksiyon olsun. "x ÎA için ¦(x+T) =¦(x) eşitliğini sağlayan bir T gerçek sayısı varsa, ¦ fonksiyonuna periyodik fonksiyon, T gerçek sayısına da ¦’ nin bir periyodu denir. T gerçek sayısının en küçüğüne ise esas periyodu denir.

Buradan (bilgi yelpazesi.net)  hareketle;

k Î Z olmak üzere "aÎ IR için;

cos(a + k.2p) = cosa   ve   sin(a + k.2p) = sina   olduğundan sinüs ve kosinüs fonksiyonlarının periyodu k.2p ve esas periyodu 2p  dir.

Aynı şekilde;

k Î Z olmak üzere  a¹p/2 +kp ve a Î IR için  tan(a + k.p) = tana

k Î Z olmak üzere  a¹kp ve a Î IR için  cot(a + k.p) = cota   olduğundan tanjant ve kotanjant fonksiyonlarının periyodu k.p ve esas periyodu p  dir.

 

 

 

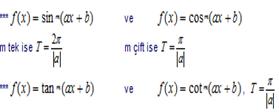
Dik Üçgende Trigonometrik Oranlar:

 

 

 

30⁰ , 45⁰ , 60^o nin trigonometrik oranları

 

 

 

 

 

 

 

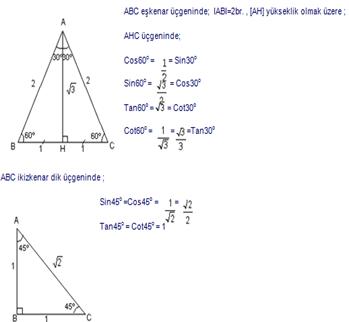
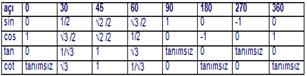
TRİGONOMETRİK FORMÜLLER

 

Trigonometrik Bağıntılar

 

 

 

Trigonometrik Özdeşlikler

 

 

 

 

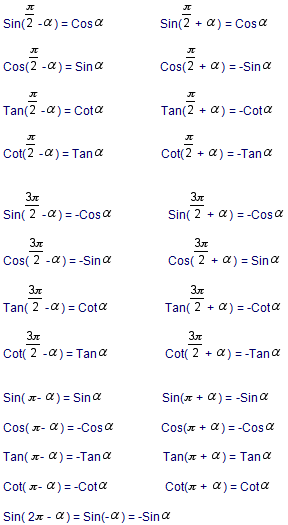
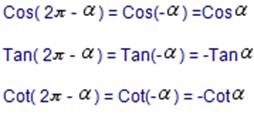
Cos, Sinüs Ve Tanjant Teoremleri

 

 

 

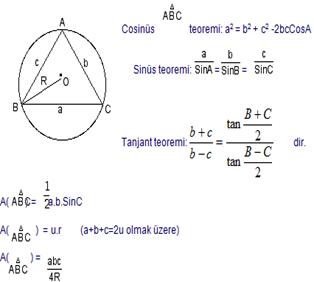
Trigonometrik Fonksiyonlarin Birbiri Cinsinden İfadesi:

 

 

 

 

 

 

Kök Formülleri:

 

 

 

Trigonometrik Denklemleri:

 

aÎ[-1,1] için cosx=a denkleminin çözümü:

Denklemin [0,2p) aralığında bir kökü a ise, Ç={x½x=a+2kp  veya  x= -a +2kp,  kÎZ}  olur.

 

Örnek:

Cosx=1/2  denkleminin çözüm kümesini bulalım.

[0,2p) aralığında kosinüsü 1/2 olan gerçek sayılar p/3 ve -p/3  olduğu hatırlanırsa;

 

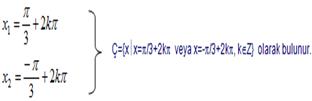
Örnek:

Cosx=Ö2/2  denkleminin çözüm kümesini bulalım.

[0,2p) aralığında (bilgi yelpazesi.net) kosinüsü Ö2/2 olan gerçek sayılar p/4 ve -p/4  olduğu hatırlanırsa;

Ç={x½x=p/3+2kp  veya x=-p/3+2kp, kÎZ}  olarak bulunur.

 

 

aÎ[-1,1] için sinx=a denkleminin çözümü:

Denklemin [0,2p) aralığında bir kökü a ise, Ç={x½x=a+2kp  veya  x= (p - a) +2kp,  kÎZ}  olur.

 

 

Örnek:

sinx=Ö3/2  denkleminin çözüm kümesini bulalım.

[0,2p) aralığında sinüsü Ö3/2 olan gerçek sayılar p/3 ve p-p/3  olduğu hatırlanırsa;

 

Örnek:

sinx=0  denkleminin çözüm kümesini bulalım.

[0,2p) aralığında sinüsü 0 olan gerçek sayılar 0 ve p  olduğu hatırlanırsa;

Ç={x½x=kp, kÎZ}  olarak bulunur.

 

 

aÎR  için tanx=a denkleminin çözümü:

Denklemin [0,2p) aralığında bir kökü a ise, Ç={x½x=a+kp,  kÎZ}  olur.

 

Örnek:

tanx=Ö3  denkleminin çözüm kümesini bulalım.

[0,2p) aralığında sinüsü Ö3/2 olan gerçek sayılar p/3 ve p/3 +p  olduğu hatırlanırsa;

Ç={x½x=p/3+kp, kÎZ}  olarak bulunur.

 

 

aÎR  için cotx=a denkleminin çözümü:

Denklemin [0,2p) aralığında bir kökü a ise, Ç={x½x=a+kp,  kÎZ}  olur.

 

 

“MATEMATİK DERSİ İLE İLGİLİ KONU ANLATIMLAR” SAYFASINA GERİ DÖNMEK İÇİN

>>>TIKLAYIN<<<

“MATEMATİK DERSİ İLE İLGİLİ TEST SORULARI, SORU BANKASI” SAYFASINI GÖRMEK İSTERSENİZ

>>>TIKLAYIN<<<

“MATEMATİK DERSİ İLE İLGİLİ YAZILI SORULARI” SAYFASINI GÖRMEK İSTERSENİZ

>>>TIKLAYIN<<<

EKLEMEK İSTEDİKLERİNİZ VARSA AŞAĞIDAKİ "Yorum Yaz" kısmına ekleyebilirsiniz.